Minimum Votes to Win the Electoral College
With a Republican once again winning the electoral college despite losing the popular vote, I was wondering, what, mathematically, is the fewest number of ballots needed to win the electoral college?
My first approach was to rank the states in order of votes per electoral vote, and assign the states with the fewest ballots per EV to one candidate until that candidate has enough electoral votes to win.
I found an interesting source of data in the United States Elections Project: They have already tallied in one spreadsheet not just the population of each state or the number of registered voters, but the projected actual number of ballots counted, including outstanding provisional / mail-in ballots. Since the goal is to compare electoral votes to popular vote outcomes, the number of votes cast by state seems the most relevant data to answer the original question. So, I used their estimated 2016 November General Election Turnout data, retrieved the morning of November 12th.
I put those in a spreadsheet which contains the number of electoral votes by state, added a calcualted column Ballots per EV = Ballots / Electoral Votes, sorted by Ballots per EV in ascending order, and marked the first 32 states as belonging to the electoral vote winner.
In the winner's states (marked as Republican [red] in the map below), I assigned the winner 50.01% of the vote, and the loser the remainder. In the rest of the states, I assigned the winner 0% of the vote, and the loser 100% of the vote. This of course is an impossible outcome in real life, but this is math, not real life!
This resulted in 30 million votes going to the electoral college winner out of 133 million votes cast: The winner won with only 22.5% of the votes.

Maps generated at 270 To Win.
Given that the intent is to produce the most electoral votes from the fewest total votes, I found it interesting that this scenario included in the winner's column many larger states that are typically thought of as underrepresented, including 3 of the 5 most populous states: California, Texas, and New York. But that intuition is based on a measure of population per electoral vote. The many factors that prevent residents from becoming voters - citizenship status, age, and voter enthusiasm to bother voting - reduce the total number of ballots cast in these states by more than most, and moved the voters in these states to in fact be slightly over-represented in the critical metric of ballots per electoral vote. I imagine enthusiasm is significantly driven by partisan makeup of the state. Florida, a swing state, gives voters far more reason to believe their vote might tip the national election, and has far more political operatives dragging voters to the polls.
But I also noticed that this solution produced a winner wih 284 electoral votes - a non-trivial amount more than the fewest electoral votes required to win. That New York was the tipping point state demonstrated that it might be necessary to un-select one state before adding the next state. I wanted to know if we could do better.
This seemed like a textbook case where the optimal solution needs to be found from among all possible ways to reach the current state, not just the most obvious one. So I whipped up a knapsack-style dynamic programming solution. For each number of electoral votes, it computers from each fewer number of electoral votes (including zero) which state, if any, can most efficiently reach the curent number of electoral votes. That is:
For EV_count in 1 to 538
Mark ev_count as having no solution
For subproblem in 0 to EV_count - 1
ev_gap = EV_count - subproblem
possible_states = states with ev_gap votes not in solution(subproblem)
best_state = state in possible_states with fewest ballots per electoral vote
If ballots(solution(subproblem) + best_state) < ballots(solution(ev_count))
let solution(ev_count) = solution(subproblem) + best_stateAgain assigning 50.01% of the winner's states' votes to the winner, and 100% of the loser's states' vote to the loser, the solution this found required about 2.5 million votes fewer to win: 27.5 million out of 133 million cast, or 20.7% of the total ballots cast. It did this by substituting the 22 electoral votes of Arizona and Indiana with Louisiana's 8 electoral votes, creating a solution with exactly 270 electoral votes. While an impossible scenario in any political reality (let alone the one we exist in), it is impressive just how unrepresentative of public preference the electoral college could get.
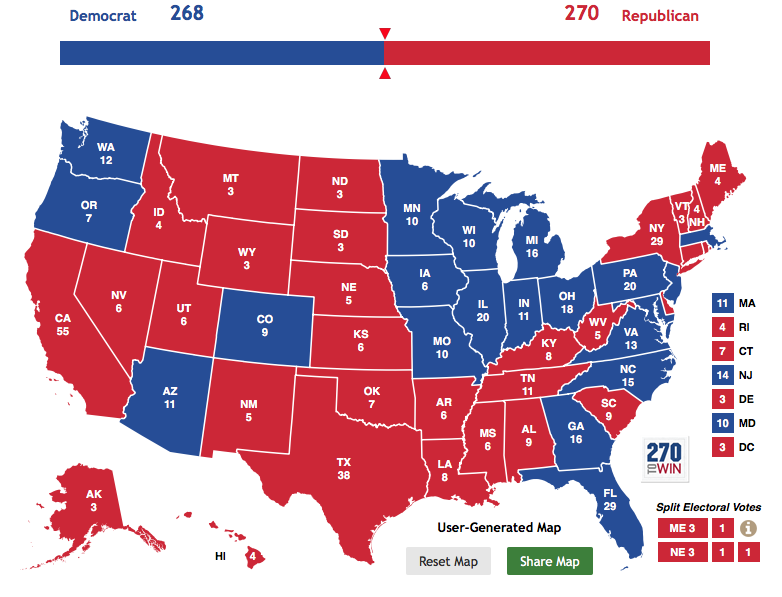
Map generated at 270 To Win.
Is it inevitable that the best winning solution would have exactly 270 votes? Perhaps not. I also printed out the minimum ballots to reach every other electoral vote total, and there were in fact three non-trivial such totals that required fewer ballots than the optimal solution for one fewer electoral vote (at 489, 498, and 508 electoral votes).
For this exercise, I broke out the states who assign electoral votes based on congressional district into separate "states" for the at-large and congressional-district based electoral votes by dividing the at-large ballots in half and assigning the other half of those ballots to the congressional-district based 'states' proportionally to the number of votes cast in those districts. I did not attempt to prevent any 'silly' cases such as an at-large winner who did not win any congressional districts, but fortunately the optimal solution did not require me to do so.
A list of the states assigned to the winner:
- Alabama
- Alaska
- Arkansas
- California
- Connecticut
- Delaware
- District of Columbia
- Hawaii
- Idaho
- Kansas
- Kentucky
- Louisiana
- Maine (At-Large and Congressional District-based)
- Mississippi
- Montana
- Nebraska (At-Large and Congressional District-based)
- Nevada
- New Hampshire
- New Mexico
- New York
- North Dakota
- Oklahoma
- Rhode Island
- South Carolina
- South Dakota
- Tennessee
- Texas
- Utah
- Vermont
- West Virginia
- Wyoming
Resources:
- evpack.pl, a knapsack implementation of the problem in Perl. No, it's not especially elegant code.
- states.txt, state data I used, in tab-delimited format
- MinVote.numbers, a spreadsheet used for the first pass, with vote assignments modified for the results of the second pass.
But it's not as bad as it looks!
A little bit of bonus content for those who dare to click the Comments link.
Interestingly, if you eliminate the supposition that the winner gets 0% of the vote in any state they lose, and instead allocate 49.99% of the vote to them (the same percentage that the election loser won in the states the election winner wins), even with this optimized electoral vote allocation, the winner needs 49.6% of the popular vote - a mere 4/10ths of a percent short of a majority.
So, that does demonstrate that the electoral college's purpose — to reward broad support over deep support — continues to be achieved centuries later. And any commentary on who is selected is really commentary about the people who cast their ballots, not the system in which our elections operate.
Electoral College
From what I found out about the electoral college, it is a process in which a certain number of people (electors) allocated from each state who get to vote for the President of the United States, who are chosen by the people of that state. So, in fact, when the American citizens vote during the Presidential election, they actually get to elect the electors who represent the people of their respective state, not the President. The citizens while voting get to choose between the candidates when do pick a candidate, that’s like an instruction to the electors to cast the vote on their behalf. People expect their votes to reach out to their candidates, they expect their pick to get that vote. But that might not even happen. Majority of the states choose their electoral votes on the basis of the maximum number of individual votes from their citizens. Let’s take an example of how this might come into play. California has a long running history of being a democratic state which is good for the democrats as they contribute 55 electoral votes out of the total 538 but not for the republicans. Even though the republicans vote, their vote doesn’t count since the democrats scored the majority of votes leading them to win all 55 electoral votes. Now as a democrat, this is a good thing to me. But to a republican, that would hurt. Republican or Democrat or whatever other parties, I think an individual’s vote should matter. It’s not just that, just because the electoral votes were differentiated for the democratic candidate doesn’t mean, they are obligated to vote for the people’s choice. Out of 100, 87 percent of the times, it was found that the electors did not even go for what the residents of their respective state chose to be the suitable one. If that’s the case, then I don’t think the votes that the people cast would even matter which would dissuade the voters. There are plenty of smaller states which has relatively large amount of electoral votes than the entire population of the country whose main reason is the number of minimum votes that the state can have is three. This can lead to the favorite person who was supposably to be the winner to lose the election. It’s not just that because that nature of electoral college is so complex, people don’t vote. Now, electoral votes just don’t stay the same. Every 10 years, a census is taken to find out the number of people living in a particular state and depending on the increment or the decrement of the population, the electoral votes might swing either way. Electoral colleges have more influence on the ‘so-called’ swing states. Now, like I stated above, California has always been a democrat but in a similar way there are states such as Indiana who has always known to be a republican. This leads the nominees to pay more attention to the swing states since this might determine the course of the election. If looked over at the campaign held last election, data shows that both Trump and Clinton made more than ninety percent of their stops at those swing states. Out of the fifty states, eleven of them have come to been known as swing states and out of those eleven there are four swing states that hold the maximum number of votes – Florida (29), Pennsylvania (21), Ohio (20) and North Carolina (15). In this type of process, the candidate with the maximum number of popular votes does not win. We can take the 2000 Presidential election for example when George Bush despite losing to Al Gore on popular votes still won the presidency due to the maximum number of votes he received. This dissuades people from voting and the candidate who the majority of Americans want to win ends up losing which to me is not democratic. In a nutshell, what I’m trying to say is, electoral college should not be the way how the President of the United States should be chosen. Each and every vote has to count.